Auswertung
Ausreißer
Ausreißer
Eine besondere Bedeutung bei der Datenaufbereitung besitzen Ausreißerwerte. Ausreißerwerte sind Extremwerte, die sich deutlich von der erhobenen Messwertreihe abheben. Sie können einen erheblichen Einfluss auf die Datenauswertung ausüben. Abbildung 24 visualisiert die Intelligenz- und Lernleistungen von 20 bzw. 21 (mit dem Ausreißer) fiktiven Versuchspersonen. Wird der Ausreißer mit einem IQ-Wert von 150 und einer Lernleistung von 46 Punkten bei der Ermittlung der Vorhersagegerade nicht berücksichtigt, so ergibt sich ein schwacher, positiver Zusammenhang (r = 0.15) zwischen den beiden Variablen. Die dazugehörige, gestrichelte Regressionsgerade steigt folglich leicht an. Wird der einzelne Ausreißerwert hingegen mit einbezogen, ist der Zusammenhang zwischen IQ und Lernleistung leicht negativ (r = -0.17). Die dazugehörige, lineare Regressionsgerade wurde in Abbildung 24 als durchgezogene, abfallende Linie eingezeichnet.
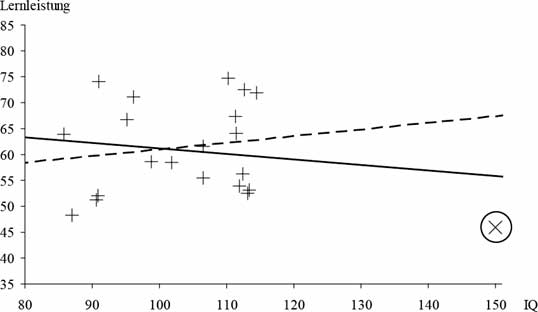
- Abbildung 24: Fiktiver Zusammenhang zwischen Intelligenz und Lernleistung in einer E-Learning Umgebung. Ein Kreuz (+) stellt eine von 20 Versuchspersonen (bzw. 21 mit Ausreißer) dar. Ohne Berücksichtigung des umkreisten Ausreißers (unten rechts) zeigt sich ein schwacher, positiver Zusammenhang (gestrichelte, ansteigende Regressionsgerade). Bezieht man den Ausreißer hingegen mit ein, so ist die Korrelation hingegen leicht negativ ausgeprägt (durchgezogene, abfallende Regressionsgerade).
Feststellung von Ausreißern
Für die Feststellung von Ausreißern existiert kein allgemein gültiges Standardverfahren. Unter anderem können folgende Methoden angewandt werden (Lohninger, 2008):
- Ermittlung über die Standardabweichungen: Diese Verfahren eignen sich vor allem, wenn die Verteilungen symmetrisch und unimodal sind.
- Bei Annahme der Normalverteilung: In diesem Fall wird ein Wert als Ausreißer betrachtet, wenn er sich 2.5 (bzw. 3) Standardabweichungen ober- oder unterhalb des Mittelwertes befindet. Den in Abbildung 24 dargestellten IQ-Wert von 150 würde man nach diesem Kriterium als Ausreißer eliminieren, da er sich etwa 3.15 Standardabweichungen über dem Mittelwert von 105.31 IQ-Punkten befindet.
- Ohne Normalverteilungsannahme: Sofern die Datenwerte keiner Normalverteilung angehören, erfolgt die Eliminierung von Ausreißern vorsichtiger. Nach dem Theorem von Tschebyschow wird ein Intervall von vier Standardabweichungen ober- und unterhalb des Mittelwertes gewählt. Diesem Kriterium zufolge wäre der in Abbildung 24 visualisierte IQ-Wert von 150 kein Ausreißer.
- Ermittlung über den Interquartilsabstand: Bei schiefen Verteilungen sollte die Feststellung von Ausreißern nicht über die Standardabweichungen erfolgen. Stattdessen
bietet sich die Ermittlung auf Basis des Interquartilsabstandes (IQR) an. Der IQR ist definiert als der Abstand zwischen dem ersten (25%) und dritten (75%) Quartil. Die Bestimmung von Grenzwerten für Ausreißer
erfolgt sodann über folgende Formel: x0.25 - 1.5 • IQR
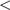 xi
xi 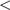 x0.75 + 1.5 • IQR. Dabei stellt x0.25 das erste und x0.75 das dritte Quartil dar. Der obere Grenzwert für das oben aufgeführte Beispiel (Abbildung 24) läge bei 138. Nach diesem Kriterium wäre der IQ-Wert von 150 als Ausreißerwert zu bezeichnen.
x0.75 + 1.5 • IQR. Dabei stellt x0.25 das erste und x0.75 das dritte Quartil dar. Der obere Grenzwert für das oben aufgeführte Beispiel (Abbildung 24) läge bei 138. Nach diesem Kriterium wäre der IQ-Wert von 150 als Ausreißerwert zu bezeichnen.
- Ermittlung über diverse Ausreißertests: Mehrere Autoren haben Tests entwickelt, um die Feststellung von Ausreißern vorzunehmen. Unter anderem kann hier der Ausreißertest nach Grubbs, der Dean-Dixon-Test, der Ausreißertest nach Walsh sowie der Nalimov-Test genannt werden. Entsprechende Formeln zu diesen Tests finden sich zum Beispiel im Internet auf den Webseiten Grundlagen der Statistik oder Wikipedia.
Manipulationsgefahr durch (fehlende) Ausreißerberücksichtigung
Durch die verschiedenen einsetzbaren Verfahren zur Feststellung von Ausreißern und den großen Einfluss einzelner Ausreißerwerte auf die Datenauswertung können die Untersuchungsergebnisse leicht in eine bestimmte Richtung manipuliert werden. Dies gilt ebenso für das absichtliche Ignorieren von Ausreißern, um etwa signifikante Befunde nicht durch Beseitigung von Ausreißern aufgeben zu müssen. Derartige Probleme sind nicht nur statistischer, sondern vor allem ethischer Natur.

 Auswertung
Auswertung